Perigal's hinged dissection demonstration of the Pythagorean theorem

Into a Macsyma input section copy and execute the definition

(c1) 
perigal(x,y):=block([equalscale:true,sq,qa,qb,qc,qd,imagdistrib:true,cy,tri,color_cycles:6./7],
 if x>y then [x,y]:[y,x],tri:[0,x,%i*y],
 qb:((qc:((qd:((qa:[0,(x+y)*%i/2,cy:-y/2+%i*y/2,(x-y)/2])-cy)*%i+cy)-cy)*%i+cy)-cy)*%i+cy,
 sq:[0,-%i*x,-%i*x+x,x],dz:x+(%i*y-x)/(%i+1)-(x-x*%i)/2,
 plot_animate(t,-%pi/2,%pi/2,block([u:(sin(t)+sin(3*t)/9)^3*729/1024+1/2,z:0,a],
  plotfaces(makelist((z:z+1,makelist(endcons(z,rectformlist(pt)),pt,face)),face,
   cons(tri,dz*u+[sq,a:qa*%e^(-%i*%pi*u/2),(qd-qd[4])*%e^(-3*%i*%pi*u/2)+a[2],
                  a:(qb-qb[2])*%e^(%i*%pi*u/2)+a[4],
                  (qc-qc[2])*%e^(3*%i*%pi*u/2)+a[4]]))))))$

Then

(c2) block([plotnum_animate:48],perigal(3,4))$

should produce

Batching the file c:\rwg\climax\cmplxlod.mac

c:\rwg\climax\simp\simp.fas being loaded.
c:\rwg\climax\base\mvars.lsp being loaded.
c:\rwg\cloe\expatch.fas being loaded.
c:\rwg\climax\library1\numth.fas being loaded.
c:\rwg\climax\ratfn\lsprimfact.fas being loaded.
c:\rwg\climax\ratfn\psqfr.fas being loaded.
Batchload done.

and then six polygons in three-space. Click on the graphic to expose a new toolbar. Click on the leftmost (camera mount) icon (Adjust graphic), then on +Z. Click off perspective (railroad tracks). Pull down the lower section boundary to a comfortable size. Click on the movie camera icon (Animate graph). Click on Cont(inuous), Bounce, speed ~ .5, then Play. You should see an oscillatory movie with these endpoints and midpoint:

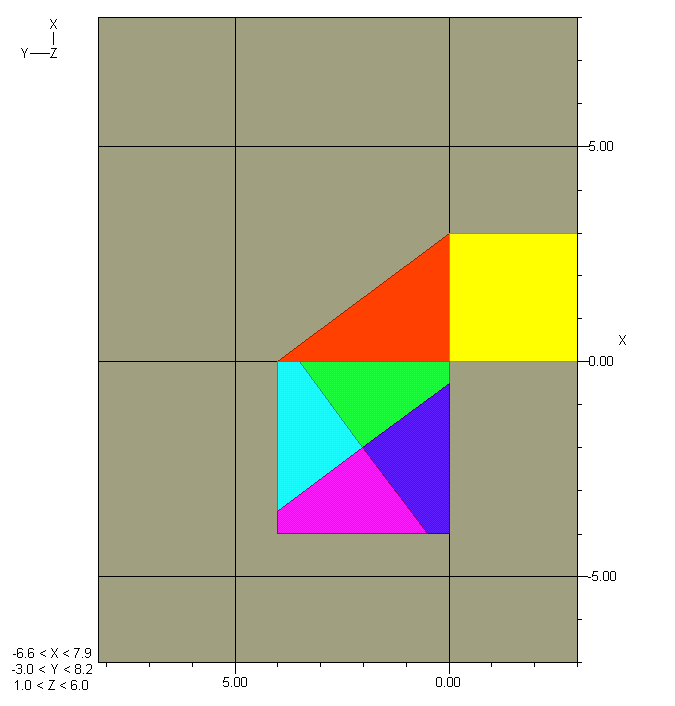
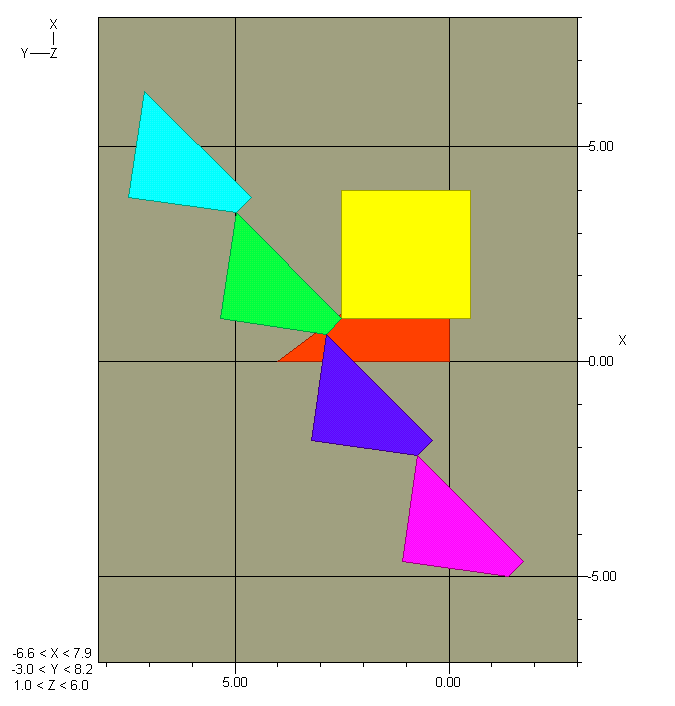
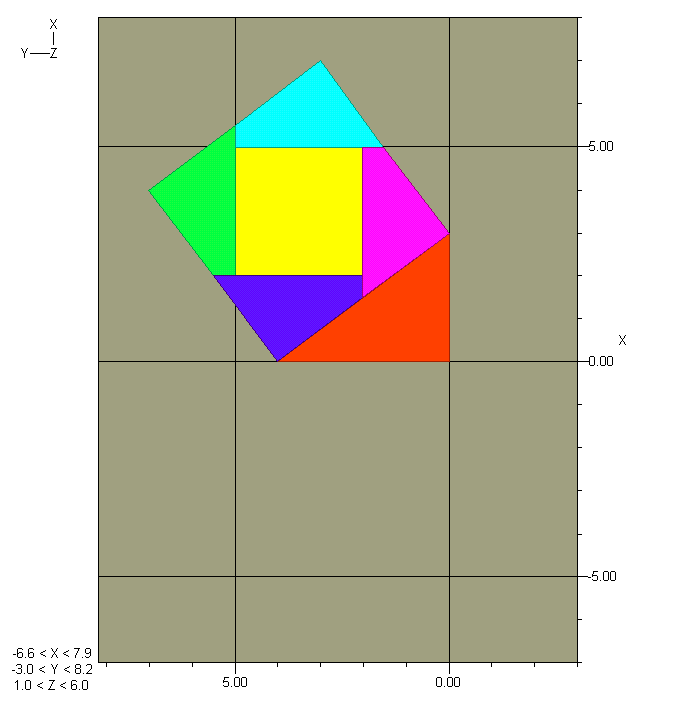
You might also try perigal(1,1) or (220,21), e.g.