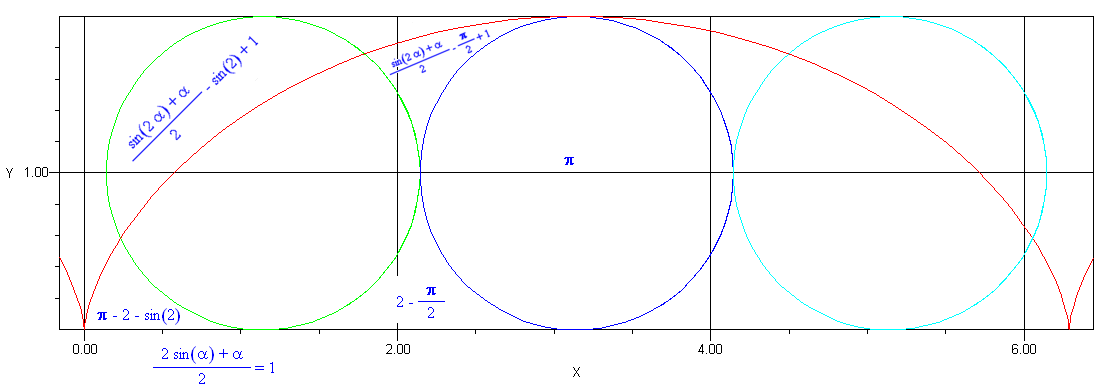
Supposedly Galileo, not knowing that the area under a cycloid was 3π, cut one from sheet metal and weighed it. (http://mathworld.wolfram.com/Cycloid.html . Perhaps 3π, or even calculus itself, was in one of Archimedes' books that was erased and overwritten with Muslim prayers.) The area of the overhanging "lune" must therefore equal the three triquetræ, although it appears to me smaller. But not as small as it is, i.e. ~0.93647316539126 < 1 < π/3 = a third of a circle. Also a bit surprising is the elementary area of the lower left triquetra, unlike the upper medial.
This is Kepler's equation with eccentricity ε=-2. See http://www.tweedledum.com/rwg/pizza.htm . The arclength is merely 8. Another vanishing π. The Fourier series is
where 
is the derivative of the usual Bessel function, and ε is the radius of the point on the rolling unit disk, 1 for the ordinary cycloid, < 1 for "oblate". The series diverges for ε > 1, the "prolate" case where the function tries to become multivalued. Here is the sum of the first nine terms for ε = 1. The blunted cusps suggest the oblate case, but this is belied by the maxima reaching 2.
